LA INTEGRAL
Desde su origen, la noción de integral ha respondido a la necesidad de mejorar los métodos de medición de áreas subtendidas bajo líneas y superficies curvas. La técnica de integración se desarrolló sobre todo a partir del siglo , paralelamente a los avances que tuvieron lugar en las teorías sobre derivadas y en el cálculo diferencial.
Concepto de integral definida

Propiedades de la integral definida
- Toda integral extendida a un intervalo de un solo punto, [a, a], es igual a cero.
- Cuando la función f (x) es mayor que cero, su integral es positiva; si la función es menor que cero, su integral es negativa.
- La integral de una suma de funciones es igual a la suma de sus integrales tomadas por separado.
- La integral del producto de una constante por una función es igual a la constante por la integral de la función (es decir, se puede «sacar» la constante de la integral).
- Al permutar los límites de una integral, ésta cambia de signo.
- Dados tres puntos tales que a < b < c, entonces se cumple que (integración a trozos):

- Para todo punto x del intervalo [a,b] al que se aplican dos funciones f (x) y g (x) tales que f (x) £ g (x), se verifica que:


Función integral

donde, para no inducir a confusión, se ha modificado la notación de la variable independiente de x a t. Esta función, simbolizada habitualmente por F (x), recibe el nombre de función integral o, también, función área pues cuando f es mayor o igual que cero en [a, b], F (x) nos da el área.

Teorema fundamental del cálculo integral
La relación entre derivada e integral definida queda establecida definitivamente por medio del denominado teorema fundamental del cálculo integral, que establece que, dada una función f (x), su función integral asociada F (x) cumple necesariamente que:

A partir del teorema fundamental del cálculo integral es posible definir un método para calcular la integral definida de una función f (x) en un intervalo [a, b], denominado regla de Barrow:
- Se busca primero una función F (x) que verifique que F¿ (x) = f (x).
- Se calcula el valor de esta función en los extremos del intervalo: F (a) y F (b).
- El valor de la integral definida entre estos dos puntos vendrá entonces dado por:
Sus principales objetivos a estudiar son:
- Área de una región plana
- Cambio de variable
- Integrales indefinidas
- Integrales definidas
- Integrales impropias
- Integral de línea
- Integrales múltiples (dobles o triples)
- Integrales trigonométricas, logarítmicas y exponenciales
- Métodos de integración
- Teorema fundamental del cálculo
- Volumen de un sólido de revolución
INTEGRACION ANTES DEL CALCULO
La integración se puede trazar en el pasado hasta el antiguo Egipto, circa 1800 a. C., con el papiro de Moscú, donde se demuestra que ya se conocía una fórmula para calcular el volumen de un tronco piramidal. La primera técnica sistemática documentada capaz de determinar integrales es el método de exhausción de Eudoxo (circa 370 a. C.), que trataba de encontrar áreas y volúmenes a base de partirlos en un número infinito de formas para las cuales se conocieran el área o el volumen. Este método fue desarrollado y usado más adelante por Arquímedes, que lo empleó para calcular áreas de parábolas y una aproximación al área del círculo. Métodos similares fueron desarrollados de forma independiente en China alrededor del siglo III por Liu Hui, que los usó para encontrar el área del círculo. Más tarde, Zu Chongzhi usó este método para encontrar el volumen de una esfera. En el Siddhanta Shiromani, un libro de astronomía del siglo XII del matemático indio Bhaskara II, se encuentran algunas ideas de cálculo integral.
Hasta el siglo XVI no empezaron a aparecer adelantos significativos sobre el método de exhausción. En esta época, por un lado, con el trabajo de Cavalieri con su método de los indivisibles y, por otro lado, con los trabajos de Fermat, se empezó a desarrollar los fundamentos del cálculo moderno. A comienzos del siglo XVII, se produjeron nuevos adelantos con las aportaciones de Barrow y Torricelli, que presentaron los primeros indicios de una conexión entre la integración y la derivación.
APLICACION
Las integrales aparecen en muchas situaciones prácticas. Considérese una piscina. Si es rectangular y de profundidad uniforme, entonces, a partir de su longitud, anchura y profundidad, se puede determinar fácilmente el volumen de agua que puede contener (para llenarla), el área de la superficie (para cubrirla), y la longitud de su borde (si se requiere saber su medida). Pero si es ovalada con un fondo redondeado, las cantidades anteriores no son sencillas de calcular. Una posibilidad es calcularlas mediante integrales.
Para el cálculo integral de áreas se sigue el siguiente razonamiento:
- Por ejemplo, consideremos la curva mostrada en la figura de arriba, gráfica de la función
 , acotada entre
, acotada entre 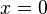 y
y 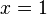 .
. - La respuesta a la pregunta ¿Cuál es el área bajo la curva de función
 , en el intervalo desde
, en el intervalo desde  hasta
hasta  ? es: que el área coincidirá con la integral de
? es: que el área coincidirá con la integral de  . La notación para esta integral será
. La notación para esta integral será
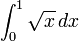 .
.
Una primera aproximación, muy grosera por cierto, para obtener esta área, consiste en determinar el área del cuadrado unidad cuyo lado lo da la distancia desde x=0 hasta x=1 o también la longitud entre y=f(0)=0 y y=f(1)=1. Su área es exactamente 1x1 = 1. Tal como se puede inferir, el verdadero valor de la integral tendrá que ser más pequeño. Particionando la superficie en estudio, con trazos verticales, de tal manera que vamos obteniendo pequeños rectángulos, y reduciendo cada vez más el ancho de los rectángulos empleados para hacer la aproximación, se obtendrá un mejor resultado; por ejem. dividamos el intervalo en cinco partes, empleando los puntos 0, 1⁄5, 2⁄5,3⁄5,4⁄5 y, finalmente la abscisa 1. Se obtienen cinco rectángulos cuyas alturas se determinan aplicando la función con las abscisas anteriormente descritas (del lado derecho de cada pedazo de la curva), así 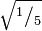 ,
, 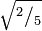 ,
, 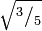 … y así hasta
… y así hasta 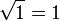 . Sumando las áreas de estos rectángulos, se obtiene una segunda aproximación de la integral que se está buscando,
. Sumando las áreas de estos rectángulos, se obtiene una segunda aproximación de la integral que se está buscando,
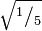 ,
, 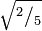 ,
, 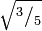 … y así hasta
… y así hasta 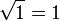 . Sumando las áreas de estos rectángulos, se obtiene una segunda aproximación de la integral que se está buscando,
. Sumando las áreas de estos rectángulos, se obtiene una segunda aproximación de la integral que se está buscando,
Nótese que se está sumando una cantidad finita de valores de la función f, multiplicados por la diferencia entre dos puntos de aproximación sucesivos. Se puede ver fácilmente que las continuas aproximaciones continúan dando un valor más grande que el de la integral. Empleando más pasos se obtiene una aproximación más ajustada, pero no será nunca exacta. Si en vez de 5 subintervalos se toman doce y ahora tomamos las abscisas de la izquierda, tal como se muestra en el dibujo, se obtiene un estimado para el área, de 0,6203, que en este caso es de menor valor que el anteriormente determinado. La idea clave es la transición desde la suma de una cantidad finita de diferencias de puntos de aproximación multiplicados por los respectivos valores de la función, hasta usar pasos infinitamente finos, o infinitesimales. La notación
concibe la integral como una suma ponderada (denotada por la "S" alargada), de los valores de la función multiplicados por pasos de anchura infinitesimal, los llamadosdiferenciales (indicados por dx).
Con respecto al cálculo real de integrales, el teorema fundamental del cálculo, debido a Newton y Leibniz, es el vínculo fundamental entre las operaciones de derivación e integración. Aplicándolo a la curva raíz cuadrada, se tiene que mirar la función relacionada 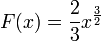 y simplemente tomar
y simplemente tomar 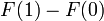 , donde
, donde  y
y  son las fronteras del intervalo [0,1]. (Éste es un ejemplo de una regla general, que dice que para f(x) = xq, con q ≠ −1, la función relacionada, la llamada primitiva es F(x) = (xq+1)/(q+1).) De modo que el valor exacto del área bajo la curva se calcula formalmente como
son las fronteras del intervalo [0,1]. (Éste es un ejemplo de una regla general, que dice que para f(x) = xq, con q ≠ −1, la función relacionada, la llamada primitiva es F(x) = (xq+1)/(q+1).) De modo que el valor exacto del área bajo la curva se calcula formalmente como
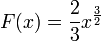 y simplemente tomar
y simplemente tomar 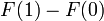 , donde
, donde  y
y  son las fronteras del intervalo [0,1]. (Éste es un ejemplo de una regla general, que dice que para f(x) = xq, con q ≠ −1, la función relacionada, la llamada primitiva es F(x) = (xq+1)/(q+1).) De modo que el valor exacto del área bajo la curva se calcula formalmente como
son las fronteras del intervalo [0,1]. (Éste es un ejemplo de una regla general, que dice que para f(x) = xq, con q ≠ −1, la función relacionada, la llamada primitiva es F(x) = (xq+1)/(q+1).) De modo que el valor exacto del área bajo la curva se calcula formalmente como
Como se puede ver, la segunda aproximación de 0,7 (con cinco rectangulitos), arrojó un valor superior al valor exacto; en cambio la aproximación con 12 rectangulitos de 0,6203 es una estimación muy por debajo del valor exacto (que es de 0,666...).
Históricamente, después de que los primeros esfuerzos de definir rigurosamente los infinitesimales no fructificasen, Riemann definió formalmente las integrales como el límite de sumas ponderadas, de forma que el dx sugiere el límite de una diferencia (la anchura del intervalo). La dependencia de la definición de Riemann de los intervalos y la continuidad motivó la aparición de nuevas definiciones, especialmente la integral de Lebesgue, que se basa en la habilidad de extender la idea de "medida" de maneras mucho más flexibles. Así, la notación
hace referencia a una suma ponderada de valores en que se divide la función, donde μ mide el peso que se tiene que asignar a cada valor. (Aquí A indica la región de integración.) La geometría diferencial, con su "cálculo de variedades", proporciona otra interpretación a esta notación familiar. Ahora f(x) y dx pasan a ser una forma diferencial, ω = f(x)dx, aparece un nuevo operador diferencial d, conocido como la derivada exterior, y el teorema fundamental pasa a ser el (más general) teorema de Stokes,
a partir del cual se deriva el teorema de Green, el teorema de la divergencia, y el teorema fundamental del cálculo.
Recientemente, los infinitesimales han reaparecido con rigor, a través de innovaciones modernas como el análisis no estándar. Estos métodos no solo reivindican la intuición de los pioneros, también llevan hacia las nuevas matemáticas, y hacen más intuitivo y comprensible el trabajo con cálculo infinitesimal.
A pesar de que hay diferencias entre todas estas concepciones de la integral, hay un solapamiento considerable. Así, el área de la piscina oval se puede hallar como una elipse geométrica, como una suma de infinitesimales, como una integral de Riemann, como una integral de Lebesgue, o como una variedad con una forma diferencial. El resultado obtenido con el cálculo será el mismo en todos los casos.
Desigualdades con integrales
- Cotas superiores e inferiores. Una función f integrable en [a, b], es necesariamente acotada en el intervalo. Por lo tanto hay dos números reales m y M tales que m ≤ f (x) ≤M para todo x de [a, b]. Dado que los sumatorios superior e inferior de f sobre [a, b] son también acotados para m(b − a) y M(b − a) respectivamente, de aquí resulta que
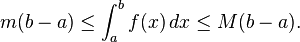
- Desigualdades entre funciones. Si f(x) ≤ g(x) para todo x de [a, b] entonces cada uno de los sumatorios superior e inferior de f son acotados inferior y superiormente por los sumatorios superior e inferior de g respectivamente. Así
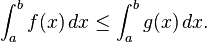
Esto es una generalización de las desigualdades anteriores, dado que M '(b − a) es la integral de la función constante con valor M en el intervalo [a, b].
- Subintervalos. Si [c, d] es un subintervalo de [a, b] y f(x) es no negativa para todo x, entonces

- Productos y valores absolutos de funciones. Si f y g son dos funciones, entonces podemos emplear su producto, potencias y valores absolutos:

Si f es Riemann integrable en [a, b] entonces lo mismo se cumple para |f|, y
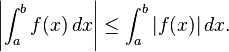
Es más, si f y g son ambas Riemann integrables entonces f 2, g 2, y fg son también Riemann integrables, y

Esta desigualdad se conoce como desigualdad de Cauchy-Schwarz, y desempeña un papel fundamental en la teoría de los espacios de Hilbert, donde el lado de la derecha se interpreta como el producto escalar de dos funciones integrables f y g en el intervalo [a, b].
- Desigualdad de Hölder. Si p y q son dos números reales, 1 ≤ p, q ≤ ∞ con 1/p + 1/q = 1, y f y g son dos funciones Riemann integrables. Entonces las funciones |f|p y |g|qtambién son integrables y se cumple la desigualdad de Hölder:
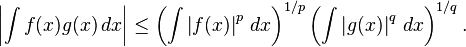
Para el caso de p = q = 2, la desigualdad de Hölder pasa a ser la desigualdad de Cauchy–Schwarz.
- Desigualdad de Minkowski. Si p ≥ 1 es un número real y f y g son funciones Riemann integrables. Entonces |f|p, |g|p y |f + g|p son también Riemann integrables y se cumple ladesigualdad de Minkowski:
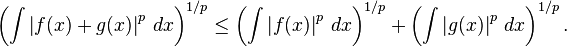
Una desigualdad análoga a ésta para la integral de Lebesgue se usa en la construcción de los espacios Lp.
Convenciones
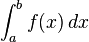
- Inversión de los límites de integración. si a > b entonces se define
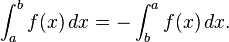
- Integrales sobre intervalos de longitud cero. si a es un número real entonces
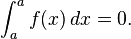
- Aditividad de la integración sobre intervalos. si c es cualquier elemento de [a, b], entonces
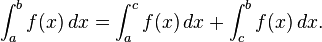
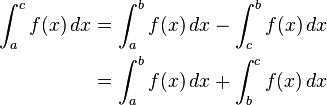

Se verifican varias desigualdades generales para funciones Riemann integrables definidas en un intervalo cerrado y acotado [a, b] y se pueden generalizar a otras nociones de integral (Lebesgue y Daniell).
sobre un intervalo [a, b] está definida si a < b. Esto significa que los sumatorios superiores e inferiores de la función f se evalúan sobre una partición a = x0 ≤ x1 ≤ . . . ≤ xn = bcuyos valores xi son crecientes. Geométricamente significa que la integración tiene lugar "de izquierda a derecha", evaluando f dentro de intervalos [x i , x i +1] donde el intervalo con un índice más grande queda a la derecha del intervalo con un índice más pequeño. Los valores a y b, los puntos extremos del intervalo, se denominan límites de integraciónde f. Las integrales también se pueden definir si a > b:
Ello, con a = b, implica:
La primera convención es necesaria al calcular integrales sobre subintervalos de [a, b]; la segunda dice que una integral sobre un intervalo degenerado, o un punto, tiene que ser cero. Un motivo para la primera convención es que la integrabilidad de f sobre un intervalo [a, b] implica que f es integrable sobre cualquier subintervalo [c, d], pero en particular las integrales tienen la propiedad de que:
- Aditividad de la integración sobre intervalos. si c es cualquier elemento de [a, b], entonces
Con la primera convención la relación resultante
queda bien definida para cualquier permutación cíclica de a, b, y c.
En lugar de ver lo anterior como convenciones, también se puede adoptar el punto de vista de que la integración se hace solo sobre variedades orientadas. Si M es una tal forma m-dimensional orientada, y M' es la misma forma con orientación opuesta y ω es una m-forma, entonces se tiene (véase más abajo la integración de formas diferenciales):



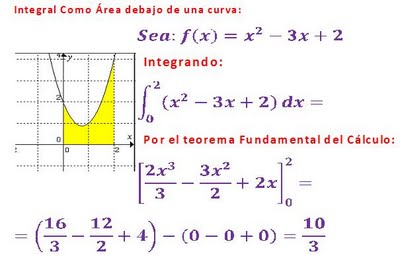
EXPLICACIÓN DE LA INTEGRAL

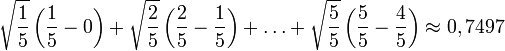
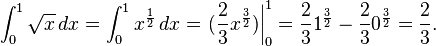

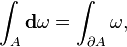
No hay comentarios:
Publicar un comentario